Light and Lenses

Using a pin hole camera we can form a clear image of a bright object. The image is clear because only a very few rays from each part of the object make it through the hole and on to the screen. This, however, makes image is dim. We can make the image brighter by using a bigger aperture (hole), this allows more rays from each part of the object to reach the screen. Unfortunately the image looks blurred as lots of images are formed, slightly offset from each other, ie light from one place on the object can reach more than one place on the screen.

To get a bright and in focus image, we need to use a lens. Lenses collect light over their entire area and bring it to a focus. Given the right distances and power of lens, it can be set so that rays from one part of the object all come together at the same point of the image.

The power of a lens is calculated by way of its focal length. The focal length is defined as the distance behind the lens that parallel rays converge to a point. The power of the lens is the reciprocal the focal length in metres. The units of lens power are dioptres, D. We can see that the more powerful the lens the shorter the distance to the focal point.

	Lenses add curvature to the wave fronts travelling through it. It does this by delaying the 'middle' of the wave front the most, as it goes through the thickest part of the lens. In fact all of the paths through the lens to the focus take the same time. The more direct routes go through more lens and so are slowed down for longer.

The curvature of a wave front (or any line) is the reciprocal of the radius of the circle that would produce that curve. We can see then that a lens adds the curvature of 1/f where f is its focal length.

1	=	1	+	1
v		u		f

Let us consider 3 specific examples of lens adding curvature: light from a distant object; light from a near object and; light from the len's focus.

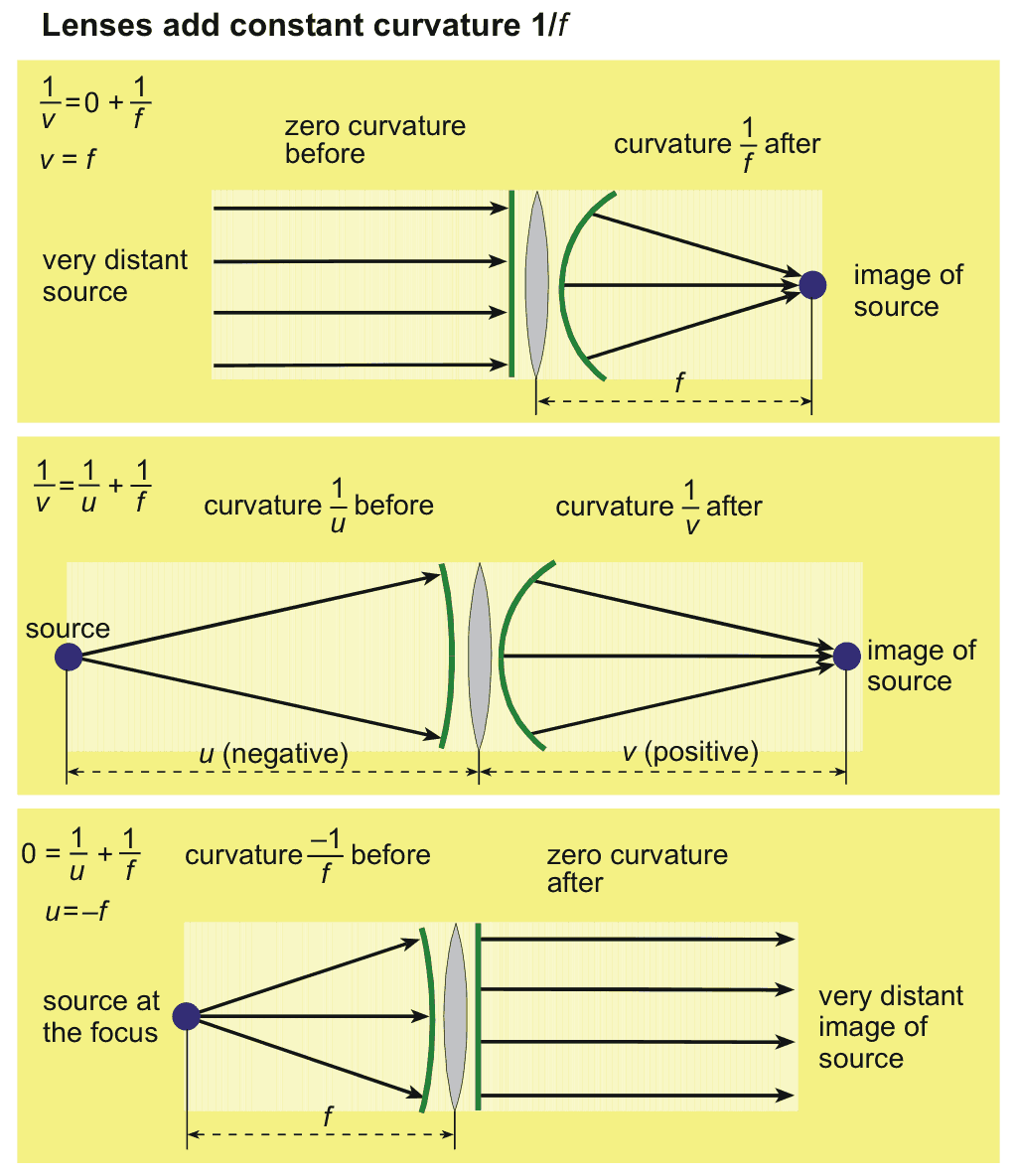
In conclusion
• Straight wave fronts will converge at the focus
• Negatively curved wave fronts will converge further away from the lens
• Light from the focus will be made parallel
• Light from a source closer to the lens than the focus will still be divergent after the lens

If the image distance (v) is greater than the object distance (u) then the image will be larger than the object. This is magnification. A negative magnification is called a diminution.

Linear magnification, m	=	image height	=	image distance	=	v
		object height		object distance		u